Tuesday, I published a critique of a paper by Council of Economic Advisers senior economist Jacob Bastian related to the debate over expanding the child tax credit (CTC). In that paper, Bastian sought to discredit analyses claiming that single mothers are highly sensitive to work incentives. Specifically, he argued that the “labor supply elasticities” used in an important paper (Corinth et al., 2022) showing that a child allowance would reduce employment by nearly 1.5 million parents were too large, overstating the predicted employment decline. He argued that if single mothers were really that sensitive to changes in work incentives, then eliminating the CTC and the earned income tax credit (EITC) would plunge their employment rate to “a level not seen since 1950.” (p. 4)
In my critique, I showed that Bastian had miscalculated the employment declines in his paper, overestimating them by nearly 50 percent. When corrected, his estimates suggest that in the absence of the CTC and EITC, employment among single mothers would go back to its early 1980s level—a reasonable finding, given that the CTC did not exist then and major EITC expansions were still to come.
Coincidentally, yesterday Bastian released a new paper that tries to make the same point—single mothers can’t be so sensitive to work incentives—from another angle. This time, he looks at episodes over the past 50 years where the work incentives faced by single mothers changed due to altered tax policy (generally due to EITC expansions, but more recently due to CTC reforms). He backs into the labor supply elasticities implied by the observed changes in work incentives among single mothers and the observed changes in their employment rates. He concludes that “unmarried mothers’ employment elasticities are around 0.3-0.4, on average” and that “[e]lasticities near 0 and above 0.7 can occasionally be found, but these are outliers.” (p. 10)
However, Bastian’s results, which bolster his own previous conclusion that the proper elasticity for single mothers is around 0.40, are again the product of a calculation error. When corrected, the proper elasticity looks more like 0.70 to 0.75. This is consistent with the literature on the topic, consistent with Corinth et al.’s elasticity of 0.75, and consistent with elasticity estimates in Bastian’s own work.
Bastian begins by calculating the mean across working single mothers of their average tax rate, doing so in every year from 1970 to 2019. Then he computes the change in this mean average tax rate over periods in which tax policy reforms altered incentives.[1] Taking the negative of this change, he calls it the average change in the return to work. This is the first ingredient he uses to determine the elasticities the data imply.
The second ingredient Bastian uses is the change in the single mother employment rate over the episodes he examines. He presents the employment rate for single mothers in every year, so he could use the changes in these rates in his calculations. However, because these employment rate changes might be due to other factors besides tax policy changes, rather than use these numbers, he relies on statistically-adjusted estimates from the EITC literature.
With these two ingredients, he calculates the elasticities during each episode of tax policy change as:
e_Bastian = (change in single mother employment as a fraction of single mothers) / [-1*(change in mean average marginal tax rate)],
where the changes are measured over episodes from 1974-75, 1986-87, 1993-96, and 2008-09.
However, there are two problems with this calculation. The elasticity is supposed to express how the percent change in employment (meaning the change in employment as a fraction of the initial number of working people) is affected by the percent change in the average return to work. Bastian has a problem in both the numerator and denominator of his estimate.
In the numerator, rather than using the change in employment rates, Bastian should be looking at the change in employment relative to the pre-policy-change employment of single mothers. That is, he should be looking at the change divided by the number of initially employed single mothers, while instead he is doing something like dividing the change by the total number of single mothers.[2] In the denominator, Bastian should be dividing the average change in the return to work by the pre-policy-change return to work (which is post-tax earnings), while he is actually doing something like dividing it by pre-tax earnings.[3]
The elasticity we want is:
e_correct = (change in single mother employment as a fraction of initially working single mothers) / (change in the average return to work as a fraction of the initial average return to work).
We can approximate the denominator[4] and compute the elasticity as
e_correct = (change in single mother employment as a fraction of single mothers) * (single mothers / initially working single mothers) / {[-1*(change in mean average marginal tax rate)] / [1-(initial mean average tax rate)]},
or
e_correct = e_Bastian * (single mothers / initially working single mothers) * [1-(initial mean average tax rate)].
This formula makes it clear that Bastian’s elasticities need to be inflated by a factor equal to the inverse of the share of single mothers initially working, multiplied by 1 minus the mean average pre-policy-change tax rate. We can obtain those quantities from his paper by eyeballing his Figures 1 and 5.[5]
The table below presents Bastian’s elasticity estimates looking at all single mothers (rather than his separate estimates by number of children). I also include my corrected estimates. Bastian’s elasticities (in Column 5) are computed by dividing Column 1 by Column 3 and multiplying it by -1. Consistent with his conclusion, the average of Bastian’s estimates in the table is 0.42 to 0.43 (depending on whether or not we exclude the lowest and highest estimates observed).
My corrected estimates (Column 6) divide Column 5 by Column 2 and then multiply by (1-Column 4). I find the average elasticity is 0.77 to 0.80.
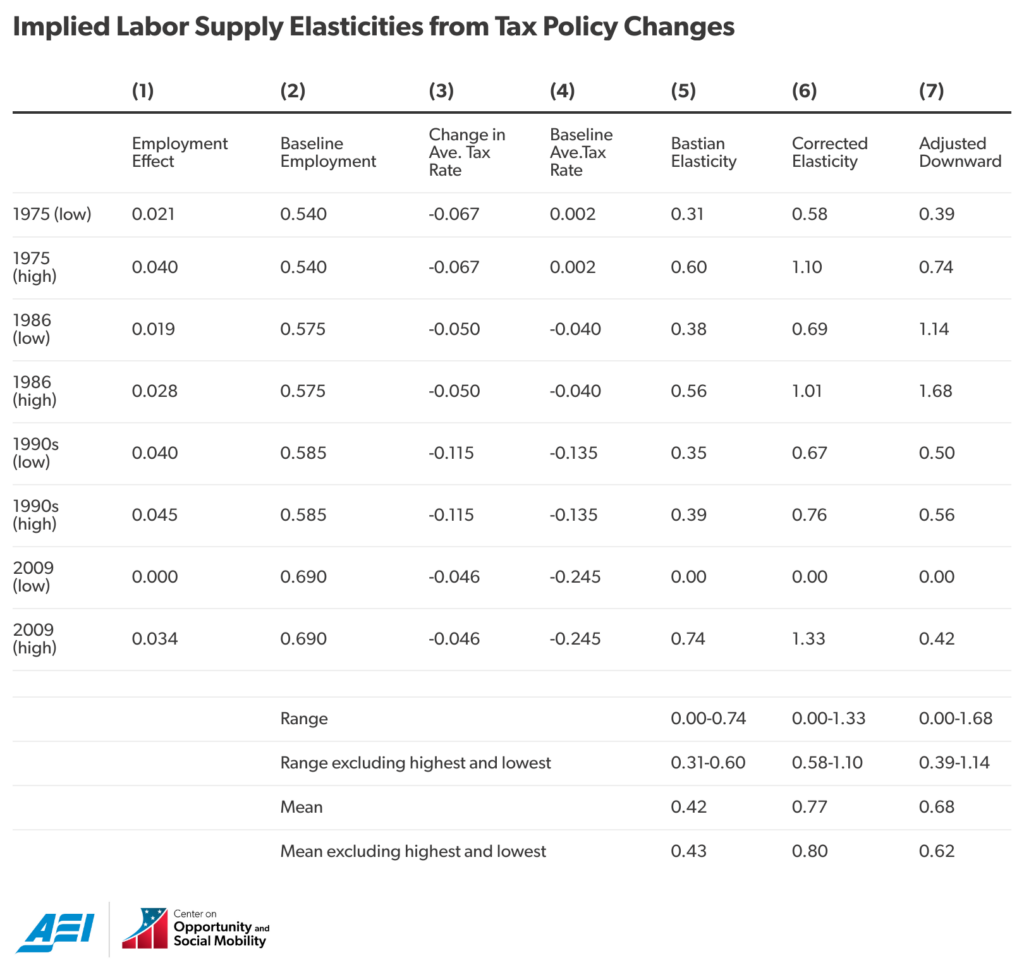
As Bastian notes, his return-to-work estimates measure the average return to work among single mothers observed to be working. Bastian notes that changes in the return to work would likely be larger for single mothers initially not working than those he calculates, which would make the resulting elasticity estimates smaller. He shows how this would affect his estimates by computing annually the 25th percentile of the distribution of average tax rates and then using the change in the 25th percentile for his change-in-return-to-work estimate rather than using the change in the mean average tax rate.
In the last column of the table, I adjust my estimates downward by the same factor implied by comparing Bastian’s estimates based on the 25th percentile and mean return-to-work.[6] The resulting estimates vary widely but the mean is 0.62 to 0.68, depending on whether or not the highest and lowest observations are included.
Across the sixteen elasticities that I estimate, the average is 0.72, again, very close to Corinth et al.’s 0.75. As another reference point, in a review with Kevin Corinth (cited by Bastian), I determined that the mean elasticity for single mothers in the research literature is 0.80 to 0.85.[7]
The evidence from Bastian’s work continues to rack up, despite his repeated efforts at refutation—single mothers are sensitive to changes in work incentives. Corinth et al.’s analyses continue to withstand challenge. An implication is that we must worry about policy changes that disincentivize work, including the CTC look-back provision in the Wyden-Smith tax bill the Senate is considering.[8]
[1] Note that the change in a mean isn’t quite the same as a mean change, in part because (in this case) the specific single mothers examined are not the same from year to year. Ideally, we would have the mean change in the average tax rate, rather than the change in the mean average tax rate. Also note that these estimates are for single mothers who are observed to be working in the data. The mean average tax rates might be different if they included non-working single mothers or were based solely on them. I return to this point later in this note.
[2] The change in employment rates is (post-policy-change employment / post-policy-change single mothers) – (pre-policy-change employment / pre-policy-change single mothers). If the number of single mothers were the same before and after the policy change, this would simplify to (post-policy-change employment – pre-policy-change employment) / single mothers.
[3] The percent change in the average return to work would be [(the change in average pretax earnings)-(the change in average taxes)]/(average post-tax earnings before the policy change). If average pretax earnings are the same before and after the policy change, this simplifies to -1*(change in average taxes)/(post-tax earnings). Bastian instead estimates (average post-policy-change taxes)/(average post-policy-change pretax earnings) – (average pre-policy-change taxes)/(average pre-policy-change pretax earnings). If average earnings are the same before and after the policy change, this simplifies to (change in average taxes)/(pretax earnings).
[4] Simplifying as in the previous footnote, under the assumption that average pretax earnings is the same before and after the policy change, the percent change in the average return to work is -1*(change in average taxes)/(post-tax earnings). This can be expressed as -1*(change in average taxes)/[pretax earnings*(1-initial tax rate)]. If, simplifying again as in the previous note, the Bastian estimate related to the change in the return to work is (change in average taxes)/(pretax earnings), then the correct change in the average return to work is the Bastian estimate divided by (1-initial tax rate). If average pretax earnings are not the same before and after the policy change, then the Bastian estimate (which is -1*(change in the marginal tax rate) divided by (1-initial tax rate) will only approximate the true change in the average return to work.
[5] I look at employment rates of single mothers and mean average tax rates in 1974, 1986, 1993, and 2008, based on the year preceding the fall in the return to work (Figure 1).
[6] For instance, his low-end 1975 elasticity using the 25th percentile is 0.21, which is two-thirds of his main result, so I reduce my elasticity by two-thirds. I do not show his elasticities based on the 25th percentile estimates in the table.
[7] Bastian’s paper also includes an abbreviated review of the literature that is selective and does not account for recent reanalyses of earlier studies. He suggests that our review finds larger elasticities because of the reanalyses we cite, but we note in our review that we get a similar conclusion that 0.75 is appropriate ignoring these reanalyses. For example, the mean estimate from the 9 reviews we include would be 0.77 using only the original estimates, while the mean from 18 papers with original elasticity estimates would be 0.66 without incorporating reanalyses. Note that Bastian makes no effort to assess the merits of the reanalyzed estimates we include, save one from a paper he coauthored (Bastian and Lochner, 2022). He now claims that the correct estimate from that paper is 0.42 rather than the 1.5 or higher that I estimated, but he provides no documentation. He says nothing about my reanalysis of Bastian and Jones (2021), which put their elasticity at around 1.5. His claim in the new paper that newer methods produce smaller elasticities is not borne out in the literature we review. His claim elsewhere that elasticities for single mothers are declining over time is not borne out by the estimates in the table above.
[8] The look-back provision would allow non-working parents to use any earnings from the previous year to qualify for a CTC, creating incentives to work one year in a given two-year period rather than two years or no years. Bastian incorrectly claims we assume that people will “choose to only work every other year” in response to the look-back provision of Wyden-Smith. (p. 10) That is a characterization that others have made in describing our results and that we corrected in a follow-up note. Bastian counters our paper’s finding that, on net, parental employment would fall by 150,000 per year by citing “economic models and most researchers” (p. 10). However, one of the sources he cites explicitly excludes the look-back provision from its modeling, stating that the authors believe the effect on work would be small without citing evidence (Durante et al., 2024). Two additional sources also assert the work effect would be small without any empirical analysis (Airi and Buhl, 2024) (Pomerleau, 2024). The last source Bastian cites is an analysis of the revenue effects of the tax bill by the Joint Committee on Taxation (2024), which does not indicate how or if a labor supply effect of the look-back provision was modeled. In a similarly uncritical fashion, Bastian cites a paper by the Center on Budget and Policy Priorities that estimates the effect of the proposed CTC reforms on child poverty (Cox, et al., 2024). That paper appears simply to assume there is no effect on work of any of the CTC revisions.